Interacting particle systems on a lattice
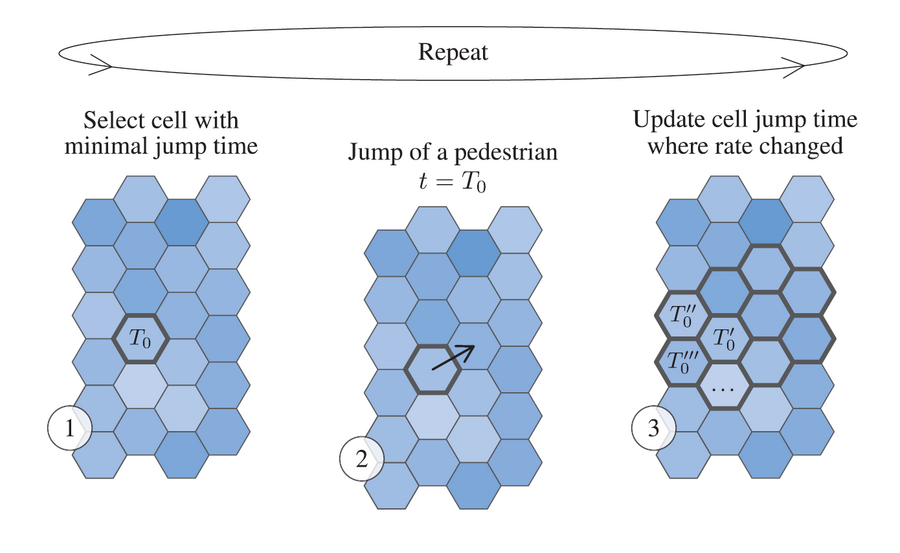
Systems of interacting particle jumping in continuous time on a lattice are well-established in statistical physics (Spitzer, 1970; Liggett, 1985). The particles jump according to, upon other variables, the state of departure and arrival sites. They are described by Markovian processes. Many pedestrian and traffic models by exclusion, zero-range, random average, or misanthrope processes exist in the literature. They can be seen as extension in continuous time of stochastic cellular automata models. Some processes (e.g. the zero-range) have product-form invariant distributions, making possible analytic descriptions of the model dynamics. Event-based simulation allow computing trajectories in continuous time. In contrast to differential systeme, no discretisation scheme are required for the simulation of the models.
Zero-range traffic model
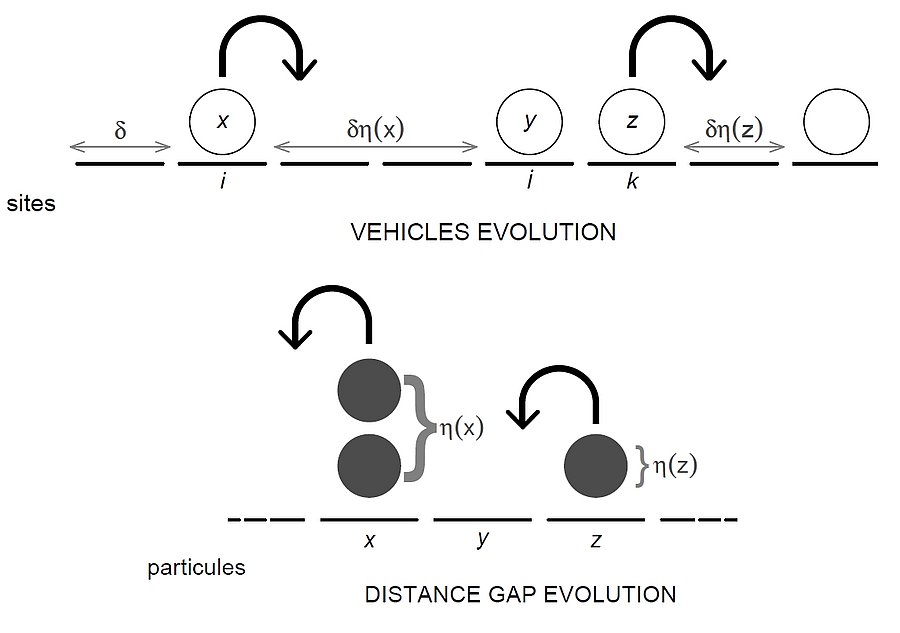
The jump rate solely depends on the number of particles on the departure site for the zero-range process introduced by Liggett in 1974. The zero-range traffic model represents each site as a vehicle and each particle as a unit of distance spacing. Basically, the speed of a vehicle depends on the distance spacing. The knowledge of the invariante product measure of the process makes possible analytical description of the asymptotic system behavior.
Totally asymmetric random average traffic model
The random average process was introduced by Roussignol in 1980. The traffic model by the totally asymmetric random average is an extension in continuous space of the traffic model by the zero-range process. The model corresponds to a stochastic event-based discretisation of a first order ODE system. The vehicle jump is random and in average proportional to the spacing. It turns out that the system has a gamma-product form invariant distribution of specific beta distributions of the spacing proportion.
Misantrope traffic model
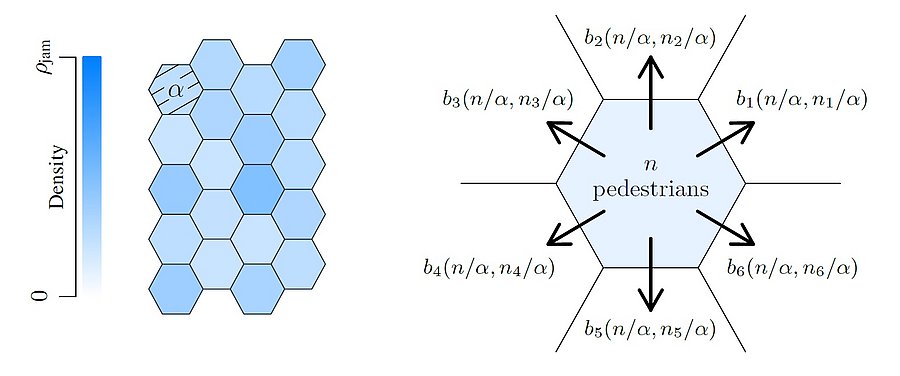
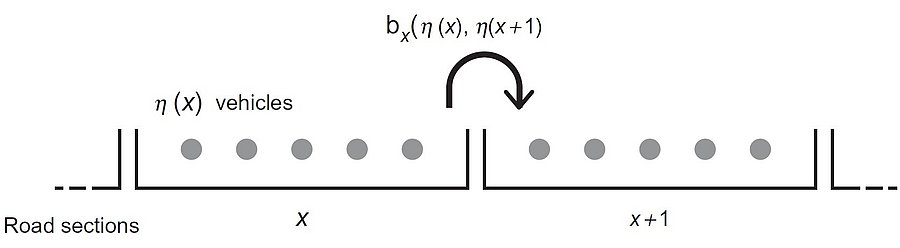
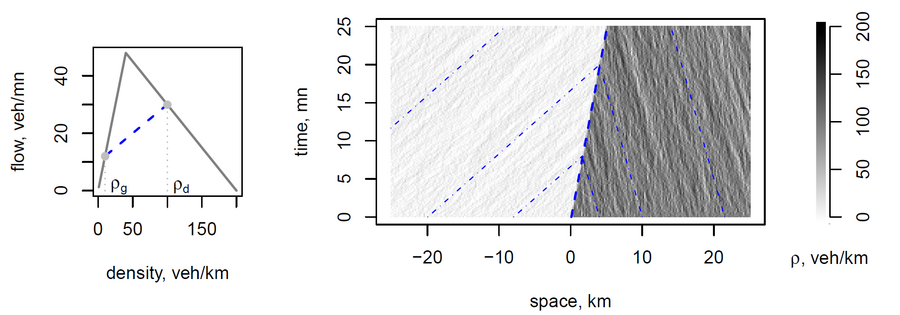
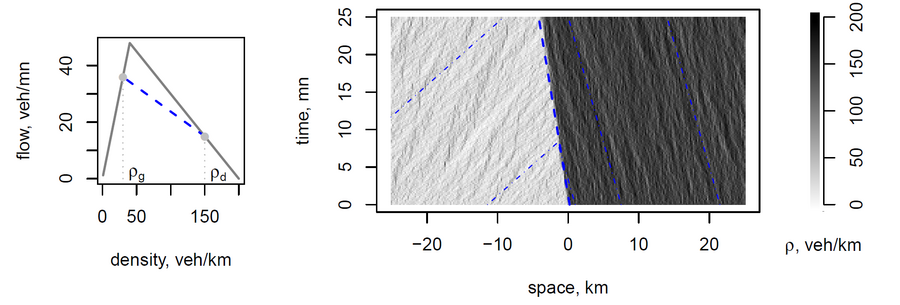
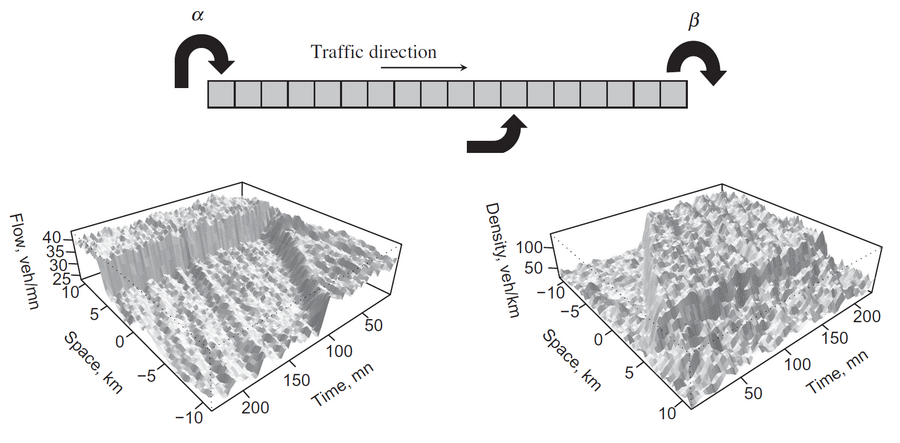
The jump rate of a particle depends on the number of particles on the departure and arrival sites for the misathrope process (Cocozza-Thivent, 1985). The rate increases as the number on the departure site increases, while it decreases as it increases on the arrival site, hence the terminology misanthrope. In the traffic flow model, a particle is a vehicle while a site is a portion of road. The system is attractive and have an unique invariante distribution that can be approximated by simulation. The process describes classical shock and rarefaction waves for Riemann problems, for which the speeds are given by the Rankine-Hugoniot formula. Indeed, continuous limits of the model are entropic solutions of the classical continuous transport problems.
- I. Ba and A. Tordeux, "Comparing Macroscopic First Order Models of Regulated and Unregulated Road Traffic Intersections" in Proceeding of 30th European Safety and Reliability (ESREL) Conference, 2021.
- A. Tordeux, G. Lämmel, F. S. Hänseler and B. Steffen, "A mesoscopic model for large-scale simulation of pedestrian dynamics", Transportation Research Part C: Emerging Technologies, vol. 93, pp. 128-147, 2018. Elsevier.
Further references
A Tordeux, M Roussignol, J-P Lebacque and S Lassarre (2014) A stochastic jump process applied to traffic flow modelling. Transportmetrica 10(4):350–375.
R Eymard, M Roussignol and A Tordeux (2012) Convergence of a misanthrope process to the entropy solution of 1D problems. Stoch Proc Appl 122(11):3648–3679.
A Tordeux, S Lassarre, M Roussignol and A Schadschneider (2011) Stationary state properties of a traffic flow model mixing stochastic transport and car-following. Proceedings of Traffic and Granular Flow’11, Springer, pp 35–46. Presentation
T M Liggett (1985). Interacting particle systems (Vol. 2). New York: Springer.
C Cocozza-Thivent (1985). Processus des misanthropes. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete, 70(4), 509-523.
E D Andjel (1982). Invariant measures for the zero range process. The Annals of Probability, 10(3), 525-547.
M Roussignol (1980). Un processus de saut sur R à une infinité de particules. In Annales de l'IHP Probabilités et statistiques (Vol. 16, No. 2, pp. 101-108).
F Spitzer (1991). Interaction of Markov processes. In Random Walks, Brownian Motion, and Interacting Particle Systems (pp. 66-110). Birkhäuser, Boston, MA.
Here is a presentation about the mesoscopic pedestrian model for large-scale simulation (2018) and here is a presentation about interactive particle systems for traffic flow (2010).